병렬 RLC회로에 대한 분석을 해보았다. 이번에는 직렬 RLC회로의 자연 응답과 계단 응답에 대해 알아보자.
직렬 RLC회로의 자연 응답
직렬 RLC회로의 자연 응답을 분석하기 위해 아래의 예시 회로를 확인해보자.

위 회로에 KVL을 적용하면 다음과 같이 나타낼 수 있다.

위의 식을 시간 t에 관해 미분하고 다시 식을 정리하면 다음과 같은 식으로 정리할 수 있다.

위의 식은 병렬 RLC회로에 대한 식을 풀어갔을 때와 동일한 형태의 식이다. 따라서 병렬 RLC에서 사용했던 이차 미분방정식의 해를 구하는 방법을 사용하면 아래와 같은 항이 0이 되어야 한다는 결과가 나온다.

위의 이차방정식을 풀면 다음의 해를 얻을 수 있다.
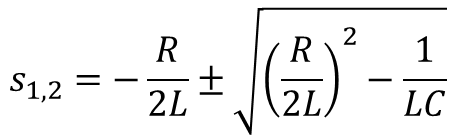
위의 식에서 공통 항을 간단하게 표현하면 다음과 같이 나타낼 수 있으며 병렬 RLC회로와 마찬가지로 α는 감쇠 주파수, 는 ω0 공진 주파수이다. 병렬 RLC회로와 감쇠 주파수는 다르지만, 공진 주파수는 같다.

병렬 RLC회로에서 분석한 것과 마찬가지로 S1,2는 세 가지 경우의 해를 가지고 있고 각각의 경우에 대해 과 감쇠, 부족 감쇠, 임계 감쇠로 분류된다.
1) α2>ω02 case, 과 감쇠(overdamped)
2) α2<ω02 case, 부족 감쇠(underdamped)
3) α2=ω02 case, 임계 감쇠(critically damped)
직렬 RLC회로의 계단 응답
직렬 RLC회로의 계단 응답을 분석하기 위해 아래의 예시 회로를 확인해보자.

위 회로에서 KVL을 적용하고 병렬 RLC회로에서 했던 것과 마찬가지로 인덕터의 시간에 대한 전류 변화량을 커패시터의 시간에 대한 전압 변화량으로 변환하여 풀어주면 결국 병렬 RLC회로의 계단 응답과 같은 형태의 해가 나온다.

직렬 RLC회로의 자연 응답과 계단 응답을 구하는 과정은 병렬 RLC회로의 자연 응답과 계단 응답을 구하는 과정과 동일하다. 병렬 RLC회로의 풀이법을 이용해 직접 직렬 RLC회로의 자연 응답과 계단 응답을 풀어보는 것을 추천한다.
'회로설계 공부 > 기초 회로이론' 카테고리의 다른 글
| [회로 기초] 라플라스 변환을 이용한 회로 해석법에 대해 알아보자 (0) | 2022.03.02 |
|---|---|
| [회로 기초] 주파수 영역에서의 수동 회로 소자 (0) | 2022.03.01 |
| [회로 기초] 병렬 RLC 회로의 자연 응답과 계단 응답에 대해 알아보자 (0) | 2022.02.27 |
| [회로 기초] 1차 RC 회로(resistor - capacitor circuit)의 계단 응답에 대해 알아보자 (0) | 2022.02.26 |
| [회로 기초] 1차 RC 회로(resistor - capacitor circuit)의 자연 응답에 대해 알아보자 (0) | 2022.02.25 |