라플라스 변환 과정에 대해서는 따로 기술하지 않고 라플라스 변환 후 회로 해석하는 방법에 대해서 알아볼 것이다.
먼저 라플라스 변환을 하는 이유는 두가지 이유가 있다. 첫 번째 이유는 우리가 지금까지 미분 방정식으로 회로를 해석해오며 어려움을 겪었는데 이 미분 방정식을 선형 다항식으로 변환해주어 해석에 어려움을 덜어주기 때문이다. 두 번째 이유는 기존에는 미분 방정식을 풀어오면서 초기 조건을 놓쳐 회로 해석에 문제가 생길 수 있지만 라플라스 변환을 하게 되면 전류와 전압의 초기값이 다항식에 자동으로 반영되기 때문에 편하기 때문이다.
앞에서 페이저 변환을 했을 때와 마찬가지로 여기서도 같은 방식으로 진행할 것이다. 회로 소자를 라플라스 변환하여 s 영역에서 표현할 것이다. 그 뒤 s영역에서 기술된 회로 소자를 이용해 지금까지 익혀온 회로 해석법에 적용되는지 확인할 것이다.
회로 소자의 s 영역 표현
저항의 s 영역 표현
먼저 저항 소자를 s 영역에서 표현해 보자. 옴의 법칙에서 R은 상수이므로 라플라스 변환식은 다음과 같다.
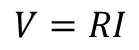
저항 소자는 시간 영역과 주파수 영역의 변환 과정에서 바뀌지않는다는 점을 알 수 있다.
인덕터의 s 영역 표현
인덕터 소자는 다음과 같이 표현할 수 있고

초기 전류를 I0라고 하면 라플라스로 변환하면 다음과 같이 표현할 수 있다.

위의 형태를 만족시키는 회로의 형태는 아래의 두가지가 있다.

두 회로 모두 같은 내용이기 때문에 차이는 없지만 개인적으로는 인덕터는 전류의 변화로 전압이 나타나기 때문에 왼쪽 전류원으로 구성된 등가 회로를 선호한다.
초기 전류가 없다면 인덕터의 s 영역 등가회로는 다음과 같이 표현할 수 있다.

커패시터의 s 영역 표현
커패시터를 라플라스 변환하면 아래와 같은 식을 얻을 수 있다. 커패시터 양단의 초기 전압은 V0로 표현했다.

위의 형태를 만족시키는 회로의 형태는 아래의 두가지가 있다.

두 회로 모두 같은 내용이기 때문에 차이는 없지만 개인적으로는 커패시터는 전압의 변화로 전류가 나타나기 때문에 오른쪽 전압원으로 구성된 등가 회로를 선호한다.
초기 전압이 없다면 커패시터의 s 영역 등가회로는 다음과 같이 표현할 수 있다.

초기 전류 및 전압은 없을 때 위 회로 소자들의 임피던스를 확인하면 다음과 같다.
| 회로소자 | 임피던스 |
| 저항 | R |
| 인덕터 | s𝐿 |
| 커패시터 | 1/sC |
라플라스 변환된 회로 소자를 사용해 회로 적용
그렇다면 s 영역을 활용하는게 어느 정도 효과적인지 예시로 RC회로의 자연 응답 분석을 통해 알아보자.
우리는 이전에 기존 방법(미분방정식)을 이용해 RC회로의 자연 응답은 해석했었다.
이번에는 s 영역을 활용해서 해석해보자.
RC 회로의 자연 응답
RC회로를 s 영역에 옮겨놓고 그려보면 아래 회로처럼 그릴 수 있다.

위의 회로에서 KVL을 적용하면 아래와 같이 표현할 수 있다.
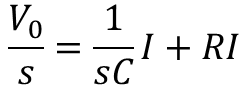
위 식을 I에 대해서 풀면 다음과 같다.

위의 표현식은 s 영역에서 표현된 식이므로 이를 t 영역으로 옮겨오면 다음과 같다. (라플라스 역변환은 생략)

전류를 기존의 방식으로 풀었던 것과 같은 결과가 나왔다.
전류의 식이 기억이 안난다면 전류에 저항 R을 곱해 저항의 식으로 만들면 더 쉽게 기억날 것이다.

이렇게 풀어보면 라플라스 변환을 하는 첫 번째 이유에 대해 이해가 된다.
또한 s 영역에서 표현하는 방식이 페이저 형식과 마찬가지로 이전에 보았던 회로 해석기법을 모두 적용할 수 있다.
임피던스끼리의 직렬연결과 병렬연결에 대한 등가 임피던스도 기존 방식대로 구할 수 있으며
회로 해석의 기본이 되었던 KCL, KVL을 적용할 수 있고 KCL과 KVL을 적용하던 회로 해석 방법인 마디 전압 법과 망 전류 법 모두 적용할 수 있다. 마지막으로 테브냉 - 노턴 등가 회로도 구현할 수 있으며 전원 변환 또한 가능하다.
앞에서 했던 회로들을 s영역에서 다시 한번 해석해보는 것을 추천한다.
'회로설계 공부 > 기초 회로이론' 카테고리의 다른 글
| [회로 기초] 직렬 RL 저역통과 필터(Low-pass filter) 에 대해 알아보자 (0) | 2022.03.07 |
|---|---|
| [회로 기초] 전달 함수(transfer function)에 대해 알아보자 (0) | 2022.03.03 |
| [회로 기초] 주파수 영역에서의 수동 회로 소자 (0) | 2022.03.01 |
| [회로 기초] 직렬 RLC회로의 자연 응답과 계단 응답에 대해 알아보자 (1) | 2022.02.28 |
| [회로 기초] 병렬 RLC 회로의 자연 응답과 계단 응답에 대해 알아보자 (0) | 2022.02.27 |