저역통과 필터(Low-pass filter)
저역통과 필터(Low-pass filter)는 입력에서 출력까지 차단 주파수(cut-off frequency) 보다 낮은 주파수의 신호를 통과시킨다. 여기서 알아볼 Low-pass filter는 수동 소자로 이루어진 필터인 수동 필터(passive filter)에 대해서만 알아보려고 한다. 먼저 수동 소자로 이루어진 Low-pass filter인 직렬 RL회로에 대해 알아보자.
직렬 RL 회로
직렬 RL 회로는 아래와 같이 구성되어 있다.

먼저, 수식을 사용하지 않고 직렬 RL회로가 어떻게 Low-pass filter가 될 수 있는지 정석적으로 분석해보자.
이 회로에서 입력인 Vi는 가변 주파수를 갖는 정현파 전압이고 회로에서 출력은 저항 양단의 전압 Vo이다.
직렬 RL 회로 - 정성적 해석
이 회로의 입력인 Vi의 주파수가 낮은 값에서부터 점차 증가한다고 가정해보자.
인덕터의 임피던스는 jωL이다. 주파수가 낮은 영역에서는 인덕터의 임피던스가 매우 낮음을 알 수 있다.
ωL≪R인 경우 이 회로에는 R의 임피던스만 존재한다고 할 수 있다.
주파수가 이제 점점 높아지면 인덕터의 임피던스가 주파수를 따라 커지게 된다. 임피던스가 커지게 되다 보면 ωL≫R인 경우부터는 이 회로에 ωL의 임피던스만 존재한다고 할 수 있다. 이 주파수가 더더욱 커지게 되어 ω=∞가 되면 인덕터의 임피던스 또한 무한히 크기 때문에 인덕터 양단이 OPEN 되어있다고 볼 수 있다.
위의 극단적인 두 경우(ω=0, ω=∞)에 대해서 회로로 표현하면 아래와 같이 표현할 수 있다.

각 극단적인 경우에 대하여 출력 전압과 위상 차이를 생각해보자.
ω=0일 때 저항 양단에 걸리는 전압 Vo는 인덕터가 SHORT 되어 입력 전압 Vi와 동일하다. 또한 인덕터가 회로에 영향을 주지 못하므로 입력 전압과의 위상 차이도 존재하지 않는다.
ω=∞일 때 저항 양단에 걸리는 전압 Vo는 회로가 OPEN 되어 전압 공급을 받지 못하므로 0이 된다. 인덕터가 회로에 영향을 주게 되므로 출력 전압은 입력 전압에 대하여 -90 º의 위상 차이를 갖게 된다.
전달 함수의 입장에서 비교하면 다음과 같이 나타낼 수 있다.
차단 주파수(Cut-off Frequency)
정성적 분석이 끝났으니 정량적 분석을 진행하기에 앞서 차단 주파수(Cut-off Frequency)에 대한 정의를 내리고 정량적 분석을 시작하려고 한다. 가장 널리 사용되는 차단 주파수 ωc의 정의는 출력의 진폭이 최대 출력 진폭의 1/√2이 되는 주파수이다.

차단 주파수의 1/√2라는 숫자가 임의로 정해진 것처럼 보일 수 있지만, 전력에 대해서 생각해보면 의미를 가진다고 볼 수 있다. 부하에서의 전압 강하가 VL일 때 부하로 전달되는 전력은 다음과 같다.

부하 전압이 최대일 때 부하로 전달되는 평균 전력을 Pmax라고 정의하면 Pmax는 다음과 같이 나타낼 수 있다.

입력 전압의 주파수를 변화하면, 회로 전달 함수의 크기가 최대가 될 때 부하 전압도 최대가 될 것이다.

이제 차단 주파수에서 평균 전력의 값을 알아보자.

위 식을 사용해 차단 주파수에서의 전력은 다음과 같다.

즉, 차단 주파수 ωc에서 부하로 전달되는 평균 전력은 최대 전력의 절반이 됨을 확인할 수 있다. 이 때문에 ωc는 1/2 전력 주파수(half-power frequency)라 불리기도 한다. 따라서 통과 주파수 대역에서 전달되는 전력은 최대 평균 전력의 50% 이상이다.
직렬 RL 회로 - 정량적 해석
이번에는 실제 전달 함수를 구해 어떻게 이 직렬 RL회로가 Low-pass filter로 동작할 수 있는지 알아보자. 직렬 RL 회로의 주파수 대역 등가 회로는 아래와 같다.

이 회로의 전압에 대한 전달 함수는 다음과 같다.

주파수 응답을 확인하기 위해 s=jω로 대체하면 다음과 같이 표현된다.

이제 위의 식을 전달 함수 크기의 식과 주파수에 대한 위상각의 식으로 분리하면 아래와 같다.
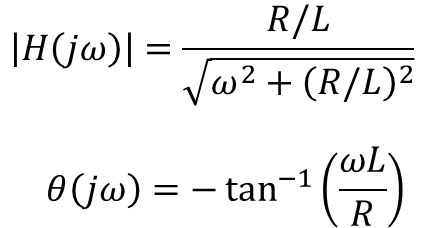
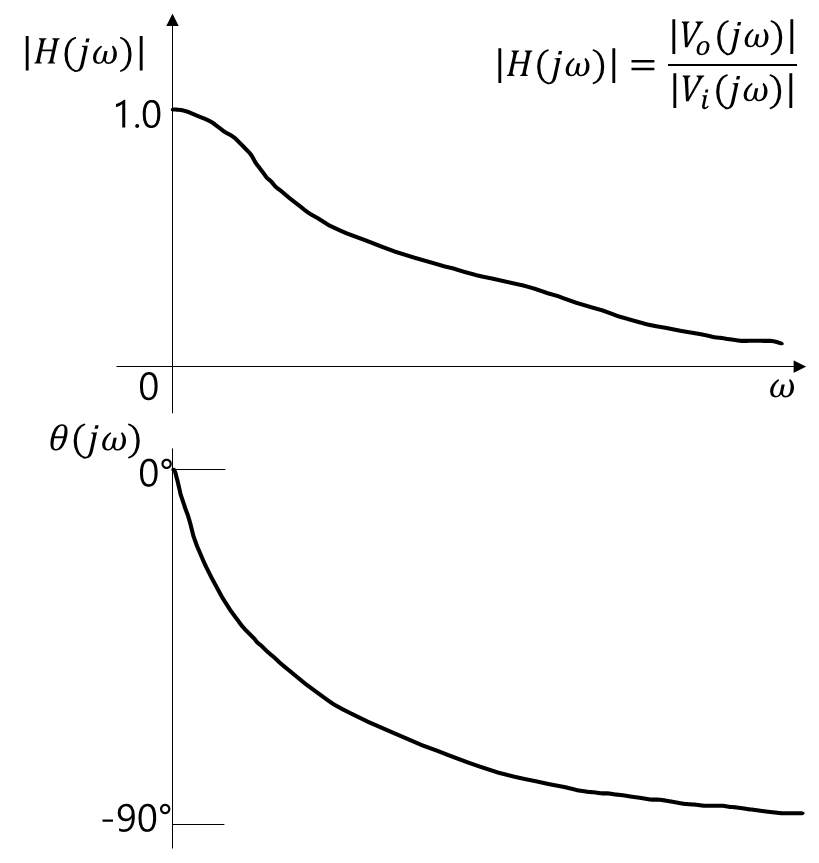
전달 함수 크기의 식을 보면 앞에서 정성적으로 분석했던 결과와 동일하다는 것을 알 수 있다.
ω=0일 때 전달 함수 크기는 1이 나와 입력과 출력이 동일하고, ω=∞일 때 전달 함수 크기는 0이 나와 정성적 분석의 결과와 동일하다. 앞서 살펴본 차단 주파수ωc에 대해서도 알아보자. 차단 주파수는 최대 출력 진폭의 1/√2이 되는 주파수이므로 다음과 같이 표현할 수 있다.
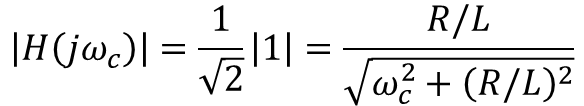
위의 식을 사용해 차단 주파수 ωc를 구하면 다음과 같이 표현할 수 있다.
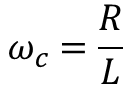
이를 보면 RL필터를 사용할 때 R과 L을 적절히 조절하면 우리가 원하는 차단 주파수를 선택하여 우리가 원하는 주파수를 통과시킬 수 있는 Low-pass filter를 설계할 수 있음을 알 수 있다.
RC회로도 RL회로와 마찬가지로 정성적/정량적 해석을 통해 분석할 수 있다. 풀어내는 방식은 동일하기 때문에 위에서 진행한 방식대로 스스로 해보면 풀 수 있을 것이다. RC회로에 대해서는 다음 장에서 해석해보자.
'회로설계 공부 > 기초 회로이론' 카테고리의 다른 글
| [회로 기초] 직렬 RL 고역통과 필터(High-pass filter) 에 대해 알아보자 (0) | 2022.03.10 |
|---|---|
| [회로 기초] 직렬 RC 고역통과 필터(High-pass filter) 에 대해 알아보자 (0) | 2022.03.09 |
| [회로 기초] 전달 함수(transfer function)에 대해 알아보자 (0) | 2022.03.03 |
| [회로 기초] 라플라스 변환을 이용한 회로 해석법에 대해 알아보자 (0) | 2022.03.02 |
| [회로 기초] 주파수 영역에서의 수동 회로 소자 (0) | 2022.03.01 |