RL회로와 RC회로에 대한 분석을 진행해보았다.
이번엔 인덕터와 커패시터를 모두 포함하는 RLC회로에 대해서 알아보자.
이번에도 마찬가지로 자연 응답과 계단 응답으로 분리해서 알아보려고 한다.
병렬 RLC회로의 자연 응답
먼저 자연 응답에 대해 알아보자.
병렬 RLC 회로를 분석하기 위해 아래의 예시 회로를 확인해보자.

위의 회로에 KCL을 적용해보면 다음과 같은 식으로 나타낼 수 있다.

위의 식을 다시 정리하면 아래와 같이 표현할 수 있다.

위 식은 2차 미분 방정식의 형태이고 2차 미분 방정식을 풀기 위해 해를 지수형으로 가정하고 풀어보면 다음과 같이 풀 수 있다.

여기서 A, s는 미지의 상수이다. 위의 변수를 식에 대입하면 다음과 같이 식을 풀어낼 수 있다.

위 식이 성립하기 위해서는 est는 0이 될 수 없기 때문에 A=0이거나 괄호 안의 항목이 0이 되어야 한다.
괄호가 0이 되려면 s로 적힌 2차 방정식을 풀어내면 다음과 같이 풀 수 있다.

위의 항에서 공통 항을 다음과 같이 표현할 수 있다.

여기서 α는 감쇠 주파수(neper fequency), ω0는 공진 주파수(resonant frequency)라고 한다.
S1, S2의 특성은 α와 ω0에 달려 있다. 여기에는 세 가지 경우가 있다.
세 가지 경우 각각의 경우에 대해 간략하게 소개하면 다음과 같다.
1) α2 > ω02 case, 과 감쇠(overdamped)
감쇠가 너무 심해 굉장히 천천히 움직이며 최종 값(정상상태)에 도달하게 된다.

2) α2 < ω02 case, 부족 감쇠(underdamped)
진동을 하지만 시간이 흐르면서 진폭이 감소해 최종 값(정상상태)에 도달하게 된다. 감쇠는 빨리 움직인다.

3) α2=ω02 case, 임계 감쇠(critically damped)
진동을 하지 않고 부드럽게 (정상상태)에 도달하게 된다.

병렬 RLC 회로의 계단 응답
병렬 RLC회로의 자연 응답에 대해 알아보았다.
이번엔 병렬 RCL회로의 계단 응답에 대해 알아보자.
병렬 RLC 회로를 분석하기 위해 아래의 예시 회로를 확인해보자.

위 회로에서 스위치가 열려있을 때 KCL을 적용하면 다음과 같은 이차 미분 방정식이 나오게 된다.
아래의 식을 유도하기 위해서는 인덕터의 전류를 v에 대해 표현하는 것이 쉽다.
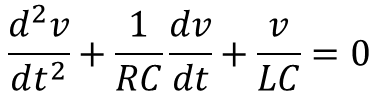
이 형태를 보면 앞에서 봤던 병렬 RLC회로의 자연 응답과 같은 형태를 가지고 있다.
병렬 RLC회로의 계단 응답의 함수는 자연 응답의 함수로 표현될 수 있다는 점이다. 다만 주의해야 할 점이 있다.
바로 이 회로는 계단 응답에 대한 함수이고 계단 응답은 결국 전원이 인가되어 있는 회로에서의 응답이다.
우리는 미분한 값을 다시 적분하는 과정에서 t=0에서의 값을 놓쳤음을 파악해야 한다.
이를 다시 이해해보면 계단 응답의 함수는 자연 응답의 함수를 포함하고 있지만 전원으로 인해 생긴 강제 응답을 더해주어야 한다는 뜻이다.
계단 응답의 결과는 다음과 같이 나타낼 수 있다.

'회로설계 공부 > 기초 회로이론' 카테고리의 다른 글
| [회로 기초] 주파수 영역에서의 수동 회로 소자 (0) | 2022.03.01 |
|---|---|
| [회로 기초] 직렬 RLC회로의 자연 응답과 계단 응답에 대해 알아보자 (1) | 2022.02.28 |
| [회로 기초] 1차 RC 회로(resistor - capacitor circuit)의 계단 응답에 대해 알아보자 (0) | 2022.02.26 |
| [회로 기초] 1차 RC 회로(resistor - capacitor circuit)의 자연 응답에 대해 알아보자 (0) | 2022.02.25 |
| [회로 기초] 1차 RL회로의 계단 응답(step response)에 대해 알아보자. (0) | 2022.02.24 |