대역 통과 필터(Band-pass filter)
지금까지 우리는 저역 통과 필터(Low-pass filter)와 고역 통과 필터(High-pass filter)에 대해 배워보았다. 두 구조 모두 차단 주파수를 기준으로 높은 쪽, 낮은 쪽과 같이 한 방향에 대해서만 통과를 시켜주었다. 이와는 달리 특정 주파수 대역만 통과시키는 구조가 대역 통과 필터(Band-pass filter)이다. 대역 통과 필터는 어떤 주파수 대역 내의 전압은 출력으로 내보내고, 대역 밖의 주파수를 갖는 전압은 걸러 내는 필터이다. 설명에서 느낌이 오겠지만 이 필터의 경우에는 두 개의 기준점이 필요하다. 이 두 개의 기준점이 대역 통과 필터의 두 개의 차단 주파수 ωc1, ωc2이다.
대역 통과 필터의 특성은 다음의 세 가지 지표로 결정된다.
1. 중심 주파수(Center frequency, ωo)
회로의 전달 함수가 실수가 되는 주파수로 정의된다. 중심 주파수는 공명 주파수(resonant frequency)라고도 부른다. 2차 RLC회로의 응답을 특정지 었던 주파수와 이름이 같고 실제로 같은 주파수이다. 회로가 공명 주파수에서 구동될 때, 구동 함수의 주파수가 회로의 고유 주파수와 같으므로, 우리는 그 회로가 공명 상태에 있다고 말한다. 중심 주파수는 통과대역의 기하학적 중심이다. 따라서 ωo=√(ωc1 × ωc2)이다.
2. 대역폭(Bandwidth, β)
통과 대역의 너비를 뜻한다. 즉, ωc1와 ωc2의 사이 간격을 의미한다.
3. 품질지수(Quality factor, Q)
대역폭에 대한 중심 주파수의 비율을 의미한다.
위의 세 가지 정의를 기억하고 이제 대역 통과 필터에 대해 알아보자.
대역 통과 필터로 동작하는 RLC회로는 아래와 같다.

이 회로에서 입력인 Vi는 가변 주파수를 갖는 정현파 전압이고 회로에서 출력은 저항 양단의 전압 Vo이다.
앞에서 LPF(Low-pass Filter), HPF(High-pass Filter)를 분석했던 것과 마찬가지로 먼저 정성적으로 분석한 뒤, 정량적으로 분석해보자.
직렬 RLC 회로 - 정성적 해석
이 회로의 입력인 Vi의 주파수가 낮은 값에서부터 점차 증가한다고 가정해보자.
ω=0일 때, 커패시터의 임피던스는 무한히 커져 커패시터 양단은 OPEN 되고, 인덕터의 임피던스는 0이 되어 인덕터 양단은 SHORT가 된다. 즉 커패시터가 회로를 OPEN 시켜 저항으로 전류가 흐르지 않게 되어 출력 전압 Vo는 0이 된다.
이제 주파수가 점점 커지게 되면, 그에 따라 인덕터의 임피던스는 증가하여 유의미한 값의 임피던스가 나오고 커패시터의 임피던스는 감소하여 유의미한 값의 임피던스가 나오게 된다. 이렇게 유의미한 값의 임피던스가 전원에 걸리게 되어 저항으로 전류가 흘러 출력 전압 Vo의 값이 나오게 된다. 이제. 주파수가 점점 더 커져 ω=∞일 때를 생각해보자.
ω=∞일 때, 커패시터의 임피던스는 0이 되어 커패시터 양단은 SHORT가 되고, 인덕터의 임피던스는 무한히 커져 인덕터 양단은 OPEN 된다. 이 때도 ω=0일 때와 마찬가지로 저항으로 전류가 흐르지 못해 출력 전압 Vo는 0이 된다.
정성적으로 해석해보면 주파수가 극으로 갔을 때는 출력 전압이 없고 주파수가 적절한 값에 들어오는 순간부터 유의미할 출력 전압 Vo를 얻게 됨을 확인할 수 있다. 이때 생길 변화 지점도 두 지점으로 예상할 수 있고, 이제 우리는 이 지점이 차단 주파수가 될 것이라는 예측을 할 수 있다.
아래 그림을 보면 이해하는데 조금 도움이 될 것이다.

아래는 정성적으로 해석한 것을 그래프로 그린 내용이다. 앞에서 본 필터의 특성을 결정하는 3가지와 연결 지어서 확인해보자.

직렬 RLC 회로 - 정량적 해석
이번에는 실제 전달 함수를 구해 어떻게 이 직렬 RLC회로가 Band-pass filter로 동작할 수 있는지 알아보자. 직렬 RLC 회로의 주파수 대역 등가 회로는 아래와 같다.

이 회로의 입력 전압에 대한 출력 전압의 전달 함수는 다음과 같다.

위 식에 s=jω을 대입하면 전달 함수의 크기와 위상각 식은 다음과 같이 나타낼 수 있다.

중심 주파수 ωo에 대해 알아보자. 중심 주파수 ωo는 전달 함수가 순 실수가 되는 주파수이다. 즉, RLC회로에서 인덕터의 임피던스와 커패시터의 임피던스의 합이 0이 되는 입력 주파수에서 순 실수가 된다.

위의 식에서 중심 주파수 ωo는 다음과 같이 나타낼 수 있다.

이번엔 차단 주파수 ωc1과 ωc2에 대해 알아보자. 차단 주파수에서 전달 함수의 크기는 최대 값의 1/√2이 됨을 이용하자.
앞에서 풀어내었던 전달 함수의 크기에 대한 식을 차단 주파수를 대입해 풀면 다음과 같이 나타낼 수 있다.

양변의 분모가 같아야 한다. 그러면 아래와 같이 풀어낼 수 있다.
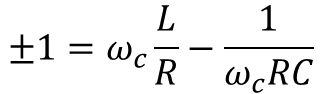
위의 식은 ωc에 대한 2개의 2차 방정식이고 해는 4개가 된다. 그중 두 개는 반드시 양수이며, 이들이 통과대역의 경계라는 의미를 가진 차단 주파수가 된다. 위의 방정식을 ωc로 풀어내면 다음과 같다.
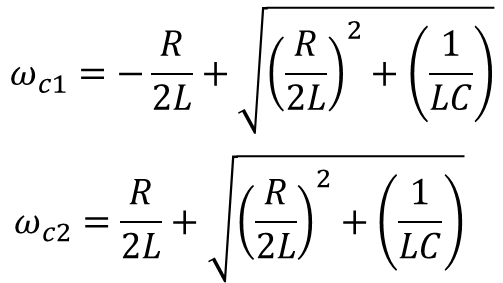
위에서 구한 차단 주파수를 사용해 중심 주파수 ωo가 차단 주파수의 기하학적 평균임을 확인해보길 바란다.
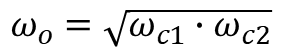
대역 통과 필터의 두 번째 지표였던 대역폭(Bandwidth)은 다음과 같이 표현할 수 있다.
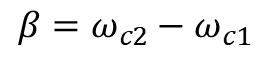
대역 통과 필터의 마지막 지표인 품질 지수는 대역폭에 대한 중심 주파수의 비로 정의된다.
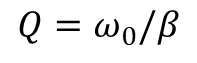
특정 주파수 대역만 통과시키는 대역 통과 필터(Band-pass Filter)에 대해 알아보았다. 대역 통과 필터에는 직렬 RLC 말고 병렬 RLC회로 구조도 존재한다. 병렬 RLC회로에서의 대역 통과 필터 구성은 다음 장에서 알아보도록 하겠다.
'회로설계 공부 > 기초 회로이론' 카테고리의 다른 글
| [회로 기초] 대역 차단 필터(Band-reject filter)에 대해 알아보자 (1) | 2022.03.13 |
|---|---|
| [회로 기초] 병렬 RLC 대역통과 필터(Band-pass filter)에 대해 알아보자 (0) | 2022.03.12 |
| [회로 기초] 직렬 RL 고역통과 필터(High-pass filter) 에 대해 알아보자 (0) | 2022.03.10 |
| [회로 기초] 직렬 RC 고역통과 필터(High-pass filter) 에 대해 알아보자 (0) | 2022.03.09 |
| [회로 기초] 직렬 RL 저역통과 필터(Low-pass filter) 에 대해 알아보자 (0) | 2022.03.07 |