Transconductance(gm)
Transconductance는 gm으로 표시한다. 전압의 변화량에 대한 전류의 변화량을 의미한다.
MOSFET에서는 Gate 전압으로 전류가 변하기 때문에 MOSFET에서의 transconductance는 다음과 같이 표현한다.
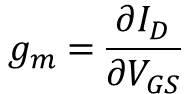
앞에서 Saturation 영역에서 MOSFET은 ideal current source로 동작할 수 있다고 얘기했다. 이 얘기를 참고해 Saturation 영역에서 transconductance 식을 살펴보면 gm이 Gate 전압에 따라 바뀐다는 것을 알 수 있다. 이는 ideal current source가 VGS의 값에 따라 흐르는 전류의 양이 바뀐다는 것을 의미한다. 그렇다면 이것은 MOSFET이 ideal current source에서 indepedent current source가 아닌 dependent current source 중 VCCS(Voltage Controlled Current Source)로 동작한다는 것을 얘기한다. 이제 Saturation 상황에서 gm을 아래 3가지 식으로 표현할 수 있다.

위의 3가지 식이 나중에 회로 설계 함에 있어 매우 많이 사용되고 자연스럽게 사용되기 때문에 자주 익혀두는 것이 좋다.
3가지 식은 각각 적용할 상황을 이해하여 사용하는 것이 중요하다. 위의 3가지 식에서 설계자가 가져갈 수 있는 변수는 3가지이다. 사이즈(W/L), 전류(ID), 전압(VGS-VTH) 이렇게 3가지이다. 그런데 각각의 식에서 이 3가지 변수 중 두 개만 적용되고 있다. 따라서 위의 식에서 두 개의 변수 중 하나의 변수가 고정되면 다른 변수에 의해서 gm을 구할 수 있다. 이를 적용하여 표현한 그래프는 아래 3가지이다.
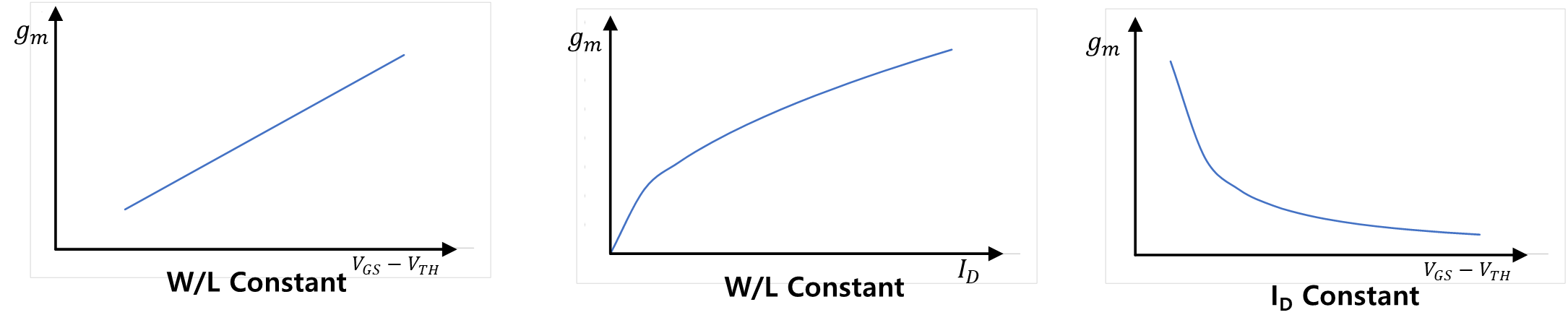
위의 3가지 그래프를 이해하고 기억하여 회로 설계 상황에 사용하자. 나의 경우에는 앞에 두 개의 그래프는 사이즈가 고정이어서 쉽게 이해가 가능했다. 마지막 그래프가 적용하는데 와닿지 않았었는데, 이렇게 생각하면 좀 쉽지 않을까 라는 생각에 첨언을 하자면 마지막 그래프는 전류가 고정일 때를 표현한 내용이다. 앞에서 본 Square-law에 따르면 전류는 변하지 않는데 VGS-VTH가 변하려면 MOSFET의 사이즈가 변경되어야 한다. 전류가 변하지 않으므로 사이즈가 늘어나면 VGS-VTH가 줄어들고 사이즈가 줄어들면 VGS-VTH가 늘어나는 형태이다. 즉, 마지막 상황은 Bias Current는 일정한 상황에서 사이즈를 변경해가는 상황으로 봐도 무방하다.
이제 Transconductance도 Drain current처럼 Drain-Source 전압에 따라 표현을 해보자.
Drain-Source 전압에 따라 VDS <VGS-VTH인 Triode Region, VDS> VGS-VTH인 Saturation Region이 있다.
두 구간에 대해서 gm을 정의에 맞춰 구해보면 다음과 같이 나타낼 수 있다.

이 장에서 중요한 것은 gm에 대한 3가지 관점을 꼭 기억해두어야 한다. 다음에 Amplifier에 대해 공부할 때 응용하기 쉬워진다. 실제로 회로를 설계함에 있어 중요한 gm을 어떻게 내 마음대로 조절할 수 있을지 가이드를 제시해주기 때문에 위의 3가지 관점은 꼭 기억해두자.
다음 장에서는 MOSFET에서 일어나는 현상들에 대해 알아보자.
'회로설계 공부 > 기초 전자회로 이론' 카테고리의 다른 글
| [기초 전자회로 이론] MOSFET의 Capacitance와 Multi Finger에 대해 알아보자. (1) | 2022.03.29 |
|---|---|
| [기초 전자회로 이론] MOSFET의 Secondary effects에 대해 알아보자. (0) | 2022.03.28 |
| [기초 전자회로 이론] MOSFET의 전압과 전류의 관계에 대해 알아보자.(3) (0) | 2022.03.26 |
| [기초 전자회로 이론] MOSFET에서 전압과 전류의 관계에 대해 알아보자.(2) (0) | 2022.03.25 |
| [기초 전자회로 이론] MOSFET에서 전압과 전류의 관계에 대해 알아보자.(1) (0) | 2022.03.24 |